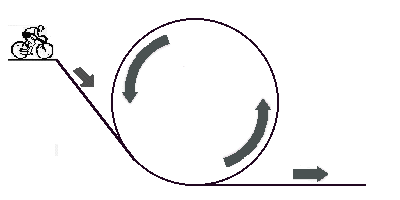26
Il ciclista
[di Filippo Spadaro]

Un mio amico ciclista vorrebbe tentare un'impresa strabiliante per la prossima festa del paese: percorrere un giro della morte sulla sua bici. Ha pensato di lanciarsi da un punto abbastanza alto per acquistare tanta velocità. La pista č posta verticalmente al terreno, e il mio amico ciclista dovrà percorrerla restando sempre all'interno della concavità. Il problema sarà quando si troverà nel punto pių alto della pista, a testa in gių e con il suo peso che tenderà a staccarlo dalla pista, facendolo cadere verso il basso, senza fargli completare correttamente l'impresa.
Il mio amico mi chiede un parere sulla fattibilà dell'impresa. Secondo voi è realizzabile?

[SOLUZIONE]

L'impresa è teoricamente realizzabile!
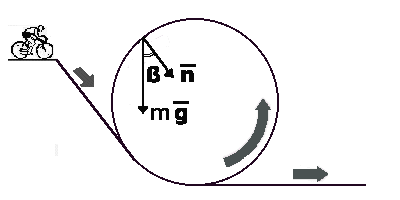Escludiamo l'ingombro della bici e ipotizziamo il mio amico ciclista tutt'uno con quel mezzo, ossia consideriamo il ciclista come un punto materiale (nel senso fisico del termine). Essendo la pista posta verticalmente al terreno, il punto critico sarà quando il ciclista si troverà nel punto più alto della pista, dove, oltre al fatto di trovarsi a testa in giù (il che di per se non dovrebbe pregiudicare l'impresa se il ciclista ha un po' di sangue freddo), dovrà anche vincere la sua forza peso, che tenderà a staccarlo dalla pista facendolo cadere in basso. Il ciclista si muove lungo la pista (tangenzialmente alla circonferenza). Mentre la condizione da imporre perché le ruote rimangano sempre appoggiate al suolo, nei punti critici della pista, è che la forza centrifuga prodotta dal ciclista sia maggiore della sua stessa forza peso. In breve, deve essere: 
   v²
m·———— > m·g·cos(ß)
   r
Dove m è la massa del ciclista, v è la velocità del ciclista, r è il raggio della circonferenza, ß è l'angolo che n (direzione normale, lungo la quale agisce la forza centrifiga) forma con la verticale, direzione lungo la quale agisce l'accelerazione di gravità g.
Risolvendo, otteniamo che deve essere (dove per sqrt() si intende l'operazione di radice quadrata): 
   v > sqrt(g·r)
Per esempio se il raggio della pista misurerà r = 3 metri, affinchè l'impresa sia realizzabile, bisognerà che il mio amico ciclista vadi ad una velocità v maggiore di appena 20 chilometri all'ora!
Ovviamente più è grande il raggio della pista, maggiore dovrà essere la sua velocità! E ipotizzando per il ciclista una velocità limite di 70Km/h, il massimo raggio considerabile per la pista potrà essere pari a 38m, fermo restando che il ciclista riesca a mantenere quella velocità percorrendo un tragitto pari ad una semicirconferenza (119m) pedalando, diciamo, a testa in giù!
Non mi resta che augurare buona fortuna al mio amico!

Logica MENTE di marzo 1999
Pagina aggiornata al 19 febbraio 1999. Autore: Filippo Spadaro